Polylogarithmic-time and constant-space-overhead fault-tolerant quantum computation with quantum low-density parity-check code
The full paper is available at: https://arxiv.org/abs/2411.03683
Introduction
Researchers at NanoQT uploaded a preprint on arXiv, “Polylogarithmic-time and constant-space-overhead fault-tolerant quantum computation with quantum low-density parity-check codes.” This work tackles a fundamental challenge in fault-tolerant quantum computation (FTQC): achieving scalable and reliable quantum computation that minimizes both qubit and time resource requirements, a key step toward practical quantum technologies.
The Challenge in Fault-Tolerant Quantum Computation
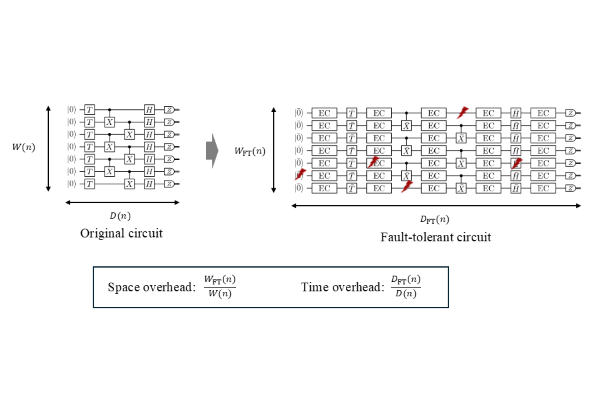
FTQC is critical for executing stable quantum computations in the presence of noise inherent in quantum systems. Traditionally, FTQC protocols have faced a trade-off between space overhead (the number of physical qubits per logical qubit) and time overhead (the physical gate operations required per logical gate). While some FTQC protocols have achieved polylogarithmic overheads in both space and time [1, 2], recent research has focused on reducing space overhead in response to the limited qubit resources in current quantum devices. However, previous approaches have faced significant challenges in maintaining low time overhead while space overhead is constant. For example, high-rate quantum low-density parity-check (QLDPC) codes incur polynomial time overhead [3, 4], while concatenated quantum Hamming codes are limited to quasi-polylogarithmic time overhead [5]. Ideally, reducing space overhead to a constant should allow time overhead to remain polylogarithmic with a higher degree. However, maintaining this balance has been challenging, highlighting the difficulty of achieving constant space overhead without imposing excessive time redundancy.
Introducing a Hybrid FTQC Protocol
Our research introduces a hybrid FTQC protocol that combines the strengths of non-vanishing-rate QLDPC codes with concatenated Steane codes, achieving polylogarithmic time overhead while maintaining constant space overhead. In this protocol, logical gates are performed through a technique known as gate teleportation. By utilizing small QLDPC codes for the robust storage of logical qubits and Steane codes for the preparation of auxiliary logical states, the protocol enables efficient implementation of logical operations. This setup supports high parallelism in the execution of logical gates, minimizing time overhead. This result eliminates the previously redundant trade-off between space and time overhead, marking a significant advancement in the field.
Threshold Theorem and Partial Circuit Reduction
The threshold theorem [6] is a foundational result in FTQC, which states that reliable quantum computation can be achieved as long as the physical error rate remains below a specific threshold. The existence of this threshold is particularly significant for building scalable quantum systems, as it implies that increasing the size of the system will not inherently increase susceptibility to errors, provided the error rate stays below the threshold.
To support our protocol, we establish a threshold theorem for FTQC with QLDPC codes using a new analytical approach called partial circuit reduction, which enables comprehensive error analysis by examining smaller, manageable subcircuits. This method resolves logical gaps in previous threshold proofs and solidifies the theoretical basis for our protocol. Importantly, unlike previous analyses that assumed instantaneous classical computations, our work explicitly considers finite classical processing times and the corresponding error accumulation. This realistic approach provides robust guarantees under practical conditions, strengthening the foundation for feasible FTQC implementations.
Conclusion
Our findings contribute to a fundamental understanding of the space-time trade-off and minimal overhead requirements for FTQC, paving the way for resource-efficient and scalable quantum computing architectures.
The team at NanoQT continues to explore the real-world applicability of this protocol and its adaptability to neutral atom systems, providing a robust foundation for future quantum hardware development.
References:
[1] P. Aliferis et al, Quantum Info. Comput. 6, 97-165 (2006)
[2] A. G. Fowler et al, Physical Review A 86 (2012).
[3] D. Gottesman, Quantum Info. Comput. 14, 1338–1372 (2014)
[4] O. Fawzi et al, in 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS) (2018)
[5] H. Yamasaki, M. Koashi, Nature Physics 20, 247–253 (2024)
