Enabling Telecomband Quantum Interconnect via Loss-Mitigation in Nanofiber Cavities
The full paper is available at: https://opg.optica.org/ol/fulltext.cfm?uri=ol-50-17-5294&id=575815
Ytterbium (Yb) is widely recognized as an ideal neutral atom qubit due to its long coherence times for quantum computing. A lesser-known but equally important advantage is its compatibility with telecom wavelengths, enabling efficient conversion to telecom photons—an essential feature for quantum communication.
We have successfully established a fabrication process for a high-finesse nanofiber cavity optimized for Yb atoms and coupled to a telecom-band transition. By effectively mitigating the excess loss of nanofiber during fabrication, this system achieves a projected cooperativity above 90, meeting practical requirements for fast and efficient atom–photon interactions. Further details are available in our paper (https://opg.optica.org/ol/fulltext.cfm?uri=ol-50-17-5294&id=575815).
Challenge in Low-loss Telecomband Nanofiber: Material Loss
Quantum interconnects serve as the photonic backbone of modular quantum computers and quantum networks, enabling entanglement across remote quantum processing units (QPUs). Nanofiber cavities are particularly attractive due to their long interaction region, suitability for integrating neutral atom arrays, and seamless integration to optical fiber networks [1,2]. However, realizing these advantages at telecom wavelengths—where fiber-optic infrastructure enables low-loss transmission over long distances—has been hindered by excess optical loss during fabrication.
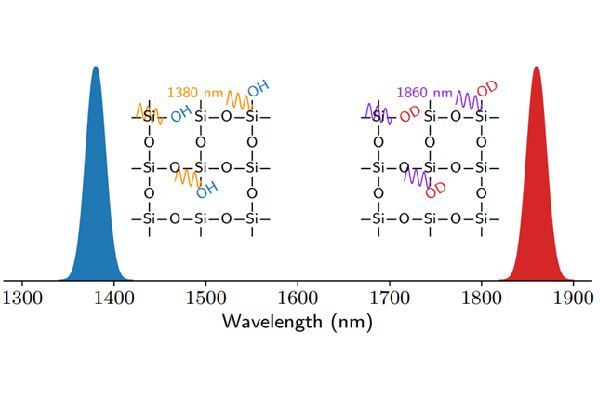
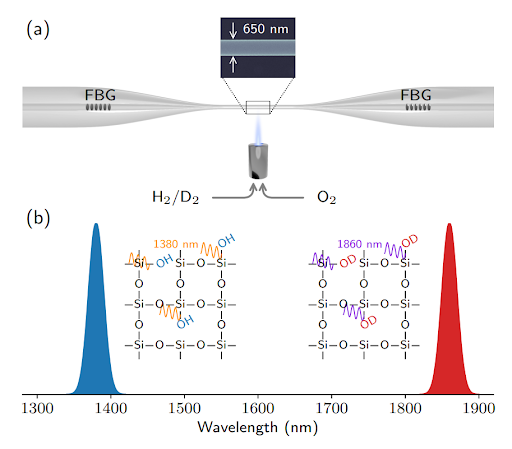
The source of this loss lies in the standard heat-and-pull method that uses a hydrogen-oxygen (H₂-O₂) flame to taper fibers [3]. This process implants hydroxyl (OH) groups into the fiber surface, which strongly absorb light near 1389 nm—a key transition wavelength for Yb qubits. This absorption severely limits the cavity finesse and cooperativity, making high-rate, high-fidelity entanglement impractical.
Mitigation Identified Through a New Fabrication method
The core insight of this study is to replace the conventional H₂-O₂ flame with a deuterium-oxygen (D₂-O₂) flame during nanofiber fabrication. This simple yet powerful substitution shifts the vibrational overtone absorption band from 1389 nm to 1860 nm, effectively bypassing the loss channel without requiring major changes to the fabrication system. The team demonstrated that this method reduces the fiber transmission loss at 1389 nm by an order of magnitude, from ~8% to <1%, at the nanofiber waist diameter of 650 nm.
Building on this method, the team fabricated a nanofiber cavity operating at 1389 nm. The cavity achieved an intrinsic finesse of 2000(100), with a round-trip loss of just 0.31(2)%. This corresponds to a cooperativity of 90 when coupled with Yb atoms—well within the regime required for fast and efficient atom-photon interactions.
Prospect of Telecomband Nanofiber-Cavity based Interconnect:
This demonstration validates the nanofiber cavity as a viable platform for quantum interconnects operating at telecom wavelengths. Since 1389 nm lies closest to the problematic OH absorption band, the success of this method at this wavelength implies that it will be even more effective at longer telecom-band transitions of Yb (e.g., 1480 nm and 1539 nm) [4,5].
Combined with prior theoretical work by NanoQT on scalable architecture of quantum interconnect based on nanofiber cavity platforms [1,2], this result paves the way for scalable, high-rate, high-fidelity quantum networking architectures using photons.
Summary
This work resolves a key fabrication bottleneck that has limited the use of nanofiber cavities at telecom wavelengths. By switching from hydrogen to deuterium during fiber tapering, the team eliminated a major optical loss channel, enabling the fabrication of high-finesse cavities compatible with Yb-based quantum interconnects. The demonstrated device offers strong atom-photon coupling in a fiber-integrated format, providing a vital building block for future quantum networks and distributed quantum computation.
References:
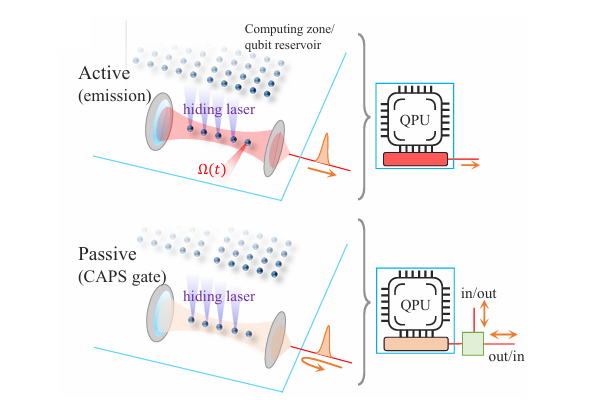
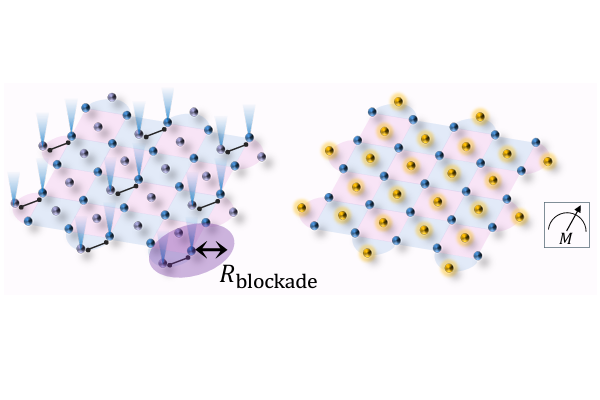
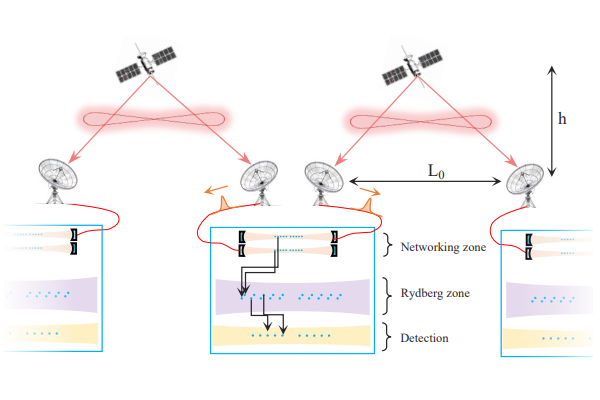
[1] S. Sunami et al., PRX Quantum 6, 010101 (2025) (Blog page)
[2] S. Kikura et al., arXiv.2502.14859 (2025) (Blog page)
[3] S. K. Ruddell et al., Opt. Lett. 45, 4875 (2020).
[4] J. P. Covey et al., Phys. Rev. Applied 11, 034044 (2019).