Introduction of Cavity QED
What is cavity QED?
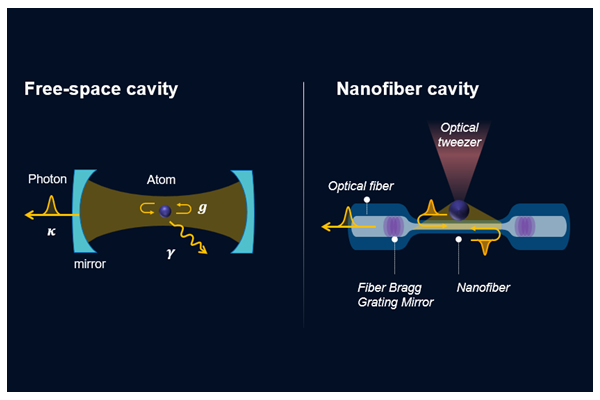
Cavity Quantum Electrodynamics (cavity QED) explores the interaction between light and matter within a confined space, or “cavity,” at the level of single photons and atoms. In the realm of cavity QED, atoms or quantum emitters are placed inside a resonant cavity, which traps photons and enhances their interaction with the atoms. The enhanced interaction within the cavity leads to a regime known as strong coupling, characterized by a profound mutual influence between single atoms and the photonic states confined within the cavity. In this regime, the presence of even a single atom can significantly alter the behavior of photons, and conversely, the photons can markedly affect the atomic states. The strong coupling condition is quantitatively characterized by a single-atom cooperativity that exceeds unity; This cooperativity C=g^2/(κ γ) is a critical measure, determined by the atom-photon coupling rate (g), the decay rate of the atomic excited state (γ), and the rate at which photons leak out of the cavity (κ), which serves as a figure of merit indicating the relative strength of coherent interactions compared to the dissipative or lossy processes within the system.
A hallmark demonstration of this strong coupling regime is the observation of vacuum-Rabi splitting. This phenomenon occurs when the coherent interaction between the atom and the photon field within the cavity overcomes the dissipative dynamics, such as spontaneous emission or cavity leakage. The result is the splitting of the energy levels into two distinct peaks, visible in the spectral output of the system. The pioneering work in observing vacuum-Rabi splitting in the optical regime was conducted by Jeff Kimble and his colleagues [1]. Their experiments not only confirmed theoretical predictions but also emphasized the potential of cavity QED systems to act as building blocks for more complex quantum networks, where controlled, coherent interactions between light and matter play a crucial role.
Simultaneously, Serge Haroche achieved strong coupling in the microwave domain, paralleling the achievements in the optical regime but using different technology and methodologies [2]. Haroche’s pioneering work involved the use of microwave cavities to confine the microwave photons, while atom-photon interaction was significantly enhanced by using atoms in high-lying Rydberg states. His pioneering efforts, along with subsequent work involving the measurement and manipulation of individual quantum systems within a microwave cavity, have been recognized with the Nobel prize in physics 2012.
Over the past decades, Cavity QED has evolved to become a fundamental building block of quantum information science, enabling controlled atom-photon interactions at the single quanta level — a capability that is indispensable for a wide range of applications, including quantum computing, quantum communication, and quantum sensing [3].
In the microwave regime, the discovery of the superconducting qubit using a Josephson junction has resulted in groundbreaking advancements in the coherent control of qubits at microwave frequencies, making them compatible with existing electronic technologies [4]. Now referred to as circuit QED systems [5], their applications in quantum computation are currently spearheaded by major corporations such as Google and IBM. Despite the rapid advancements made over the past few decades, scalability challenges continue to persist. Microwave photons are not ideally suited for transmitting information due to propagation losses in waveguides. Additionally, coherent transfer between microwave and optical photons continues to be a technically demanding task, despite numerous proposals and dedicated experimental efforts to address this issue [6].
Conversely, in the optical regime, an elementary quantum network based on cavity QED systems has been successfully demonstrated. In this setup, atoms efficiently store, process, and exchange quantum information using optical photons as carriers, facilitating entanglement generation over long distances [7, 8]. One of the promising features of the cavity QED based approach, which has yet to be demonstrated, is its potential to enable high-rate and high-fidelity entanglement distribution among distant nodes. This capability is crucial because it enables the establishment of coherent quantum states across the network, irrespective of the physical separation between individual components. Consequently, this high rate of entanglement distribution is instrumental in forming complex quantum networks towards scalable quantum computation by interconnected quantum processing units (QPUs).
Why nanofiber cavity?
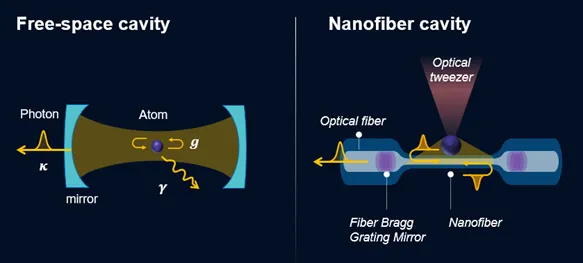
While the pioneering works have been demonstrated by using the free-space cavity, formed by a pair of bulk mirrors, the rise of nanoscale and integrated cavity technologies, such as photonic crystal cavities and whispering gallery mode resonators, enables cavity QED platforms to become a key tool in developing scalable, high-performance quantum devices [9 – 13]. Among various platforms, nanofiber cavity is one of the ideal platforms due to the strong atom-photon coupling [14], large capacity of atom number, low optical loss inside the cavity and the seamless integration into the optical fiber network [15]. We will examine each advantages in detail as follows:
Our nanofiber cavity features a mm-long nanofiber segment that connects to standard single-mode fiber through adiabatic tapered regions, and then to a pair of fiber Bragg grating (FBG) mirrors. The state-of-the-art nanofiber cavity demonstrates a single-path loss of 0.07%, corresponding to a cavity finesse of 4000 [16]. Thanks to the subwavelength confinement of the guided mode of the nanofiber, the atom-photon coupling rate is significantly enhanced along the entire length of the nanofiber. This nanofiber cavity, combined with an optical tweezer array, can accommodate a hundreds of atoms per single nanofiber cavity, with an expected single-atom cooperativity exceeding 100 for telecom-band transition of ytterbium atoms.
This large atom capacity is essential for maximizing the entanglement generation rate, since the time required for transporting and initializing atoms —a major bottleneck in interfacing atoms with nanofiber cavities— can be distributed across many sequential photon generation trials [17 – 19]. This time-multiplexed approach to entanglement generation is projected to yield a Bell pair generation rate approaching 100 kHz, which is sufficiently high for operation of modular QPUs towards scalable quantum computation. Additionally, the adaptability of the nanofiber cavity across various wavelengths, including the telecomband, facilitates long-distance communication with minimal loss, making them highly versatile for quantum network applications.
References:
[1] R. J. Thompson, G. Rempe, and H. J. Kimble, Observation of normal-mode splitting for an atom in an optical cavity, Phys. Rev. Lett. 68, 1132 (1991).
[2] M. Brune, F. Schmidt-Kaler, A. Maali, J. Dreyer, E. Hagley, J. M. Raimond, and S. Haroche, Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity, Phys. Rev. Lett. 76, 1800 (1996).
[3] H. J. Kimble, The quantum internet, Nature 453, 1023 (2008).
[4] Y. Nakamura, Yu. A. Pashkin, and J. S. Tsai, Coherent control of macroscopic quantum states in a single-Cooper-pair box, Nature 398, 786 (1999).
[5] A. Blais, A. L. Grimsmo, S. M. Girvin, and A. Wallraff, Circuit quantum electrodynamics, Rev. Mod. Phys. 93, 025005 (2021).
[6] M. Mirhosseini, A. Sipahigil, M. Kalaee, and O. Painter, Superconducting qubit to optical photon transduction, Nature 588, 599 (2020).
[7] A. Reiserer and G. Rempe, Cavity-based quantum networks with single atoms and optical photons, Rev. Mod. Phys. 87, 1379 (2015).
[8] A. Reiserer, Colloquium: Cavity-enhanced quantum network nodes, Rev. Mod. Phys. 94, 041003 (2022).
[9] T. Aoki, B. Dayan, E. Wilcut, W. P. Bowen, A. S. Parkins, T. J. Kippenberg, K. J. Vahala, and H. J. Kimble, Observation of strong coupling between one atom and a monolithic microresonator, Nature 443, 671 (2006).
[10] A. Goban et al., Atom–light interactions in photonic crystals, Nat. Commun. 5, 3808 (2014).
[11] T. G. Tiecke, J. D. Thompson, N. P. de Leon, L. R. Liu, V. Vuletić, and M. D. Lukin, Nanophotonic quantum phase switch with a single atom, Nature 508, 241 (2014).
[12] T. Ðorđević, P. Samutpraphoot, P. L. Ocola, H. Bernien, B. Grinkemeyer, I. Dimitrova, V. Vuletić, and M. D. Lukin, Entanglement transport and a nanophotonic interface for atoms in optical tweezers., Sci. (N. York, NY) 373, 1511 (2021).
[13] X. Zhou, H. Tamura, T.-H. Chang, and C.-L. Hung, Trapped Atoms and Superradiance on an Integrated Nanophotonic Microring Circuit, Phys. Rev. X 14, 031004 (2024).
[14] S. Kato and T. Aoki, Strong Coupling between a Trapped Single Atom and an All-Fiber Cavity, Phys. Rev. Lett. 115, 093603 (2015).
[15] S. Kato, N. Német, K. Senga, S. Mizukami, X. Huang, S. Parkins, and T. Aoki, Observation of dressed states of distant atoms with delocalized photons in coupled-cavities quantum electrodynamics, Nat. Commun. 10, 1160 (2019).
[16] S. Horikawa, S. Yang, T. Tanaka, T. Aoki, and S. Kato, High-finesse nanofiber Fabry–Pérot resonator in a portable storage container, Rev. Sci. Instrum. 95, 073103 (2024).
[17] W. Huie, S. G. Menon, H. Bernien, and J. P. Covey, Multiplexed telecommunication-band quantum networking with atom arrays in optical cavities, Phys. Rev. Res. 3, 043154 (2021).
[18] Y. Li and J. D. Thompson, High-Rate and High-Fidelity Modular Interconnects between Neutral Atom Quantum Processors, PRX Quantum 5, 020363 (2024).
[19] S. Sunami, S. Tamiya, R. Inoue, H. Yamasaki, and A. Goban, Scalable Networking of Neutral-Atom Qubits: Nanofiber-Based Approach for Multiprocessor Fault-Tolerant Quantum Computer, ArXiv (2024).
